Operaciones con polinomios

 Operaciones con polinomios

Es una expresión matemática constituida por un conjunto finito de variables (no determinadas o desconocidas) y constantes (números fijos llamados coeficientes), utilizando únicamente las operaciones aritméticas de suma, resta y multiplicación, así como también exponentes enteros positivos.

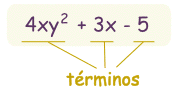
    Contienen:

	Constantes (como 3,-20, o ½)
	Variables (como x e y)
	Exponente (como el 2 en y2) pero sólo pueden ser 0, 1, 2, 3, ...etc.

También con las operaciones básicas se pueden resolver los polinomios:

·          

      SUMA DE POLINOMIOS

La suma algebraica consiste en reunir dos o más expresiones algebraicas en una sola.

Para sumar dos o más polinomios se ordenan de manera descendente y se acomoda cada polinomio de manera que cada término sea semejante, uno debajo del otro.

Ejemplo 0: Consideremos los polinomios

P(x)= 3x5 + 2x3 - 5x2 + 6 y Q(x) = 8x3 + 3x2 - x - 4

El polinomio resultante de la suma P(x) + Q(x)= 3x5 + 10x3 - 2x2 - x + 2

Fíjate, aquellos monomios cuya parte literal aparece en un polinomio los hemos copiado y hemos sumado aquellos monomios que tenían la misma parte literal:

2x3 + 8x3 = 10x3

-5x2 + 3x2 = -2x3

6 - 4 = 2

Ejercicio 1: 
Escribe el polinomio en orden descendente.

x + 6x² -1 + 5x³

Tu solución:

5x³ + 6x² + x - 1 

Ejercicio 2: 
Escribe el siguiente polinomio en orden descendente.
3x² - 5 + 4x³ - 2x

Solución:
4x³ + 3x² -2x -5 

Ejercicio 3:
 Sumar 8b-4c+2 con -3a+4b-c+1

8b-4c+2

-3a +4b - c+1

-3a+12b -5c+3

·    RESTA  DE POLINOMIOS

Para restar dos polinomios se escribe el minuendo y después el sustraendo, cambiándole los signos a cada uno de sus términos. Posteriormente se reducen los términos semejantes.

Para poder sumar o restar es necesario contar con términos semejantes (aquellos con la misma parte literal y exponente)

Ejercicio 0:
2x³ + 5x − 3) − (2x³ − 3x² + 4x)

P(x) − Q(x) = 2x³ + 5x − 3 − 2x³ + 3x² − 4x

P(x) − Q(x) = 2x³ − 2x³ + 3x² + 5x − 4x − 3

P(x) − Q(x) = 3x² + x − 3

Ejemplo 1:

Simplifica (6y² - 3y - 1) - (7y² - y) = Usar formato vertical.

Solución:       

Trata de hacerla con los pasos de arriba ;)

 

·          MULTIPLICACIÓN DE POLINOMIOS

Realizaremos una multiplicación normal pero con polinomios. Para multiplicar polinomios se multiplica cada término de un polinomio por cada uno de los términos del otro polinomio y luego se simplifican los monomios semejantes.

Se utilizan:

·         Ley de signos.

·         Los coeficientes se multiplican.

·         La ley de los exponentes para la misma base

Ejemplo 1:

Simplifica:  ( 5x + 4) (-2x)

Solución:

(5x + 4) (-2x) = -10x² - 8x 

Ejemplo 2:

Simplifica:   x³ ( 2x² - 3x + 2)

Solución:

x³ ( 2x² + -3x + 2) =  2x⁵ - 3x

               4b⁴        -2b² + 2b
                4b⁴ + 6b³ - 2b² - b + 3

DIVISIÓN DE POLINOMIOS

En este tipo de división se procede de manera similar a la división aritmética los pasos a seguir son los siguientes.

• Se ordenan los polinomios con respecto a una misma letra y en el mismo sentido (en orden ascendente u orden descendente), si el polinomio no es completo se dejan los espacios de los términos que faltan.

• El primer termino del cociente se obtiene dividiendo el primer termino del dividendo entre el primer miembro del divisor.

• Se multiplica el primer término del cociente por todos los términos del divisor, se coloca este producto debajo de él dividendo y se resta del dividendo.

• El segundo termino del cociente se obtiene dividiendo el primer termino del dividendo parcial o resto (resultado del paso anterior), entre el primer termino del divisor.

• Se multiplica el segundo término del cociente por todos los términos del divisor, se coloca este producto debajo de él dividendo parcial y se resta del dividendo parcial.

• Se continua de esta manera hasta que el resto sea cero o un dividendo parcial cuyo primer termino no pueda ser dividido por el primer termino del divisor.

Cuando esto ocurre el resto será el residuo de la división.

La intención con este método de división es que con cada resta se debe eliminar el termino que se encuentra mas a la izquierda en el dividendo o dividendo parcial.

Ejemplos:

Para poder entender más fácil el tema, veamos un vídeo:

Espero que les hay servido mucho esta información, nos vemos la próxima.

;)